人力飛行機の性能を簡単にまとめた話はよく見るものの(必要パワが何ワット、とか)、安定性・操縦性に関する練習問題みたいなものがインターネット上で簡単に手に入らないのが長年やや不満であった。不満の原因は単に自分の趣味的に安定性・操縦性のほうにより興味があるからというだけではなく(もちろんそれも多いけれど)、安定性・操縦性をあまり考慮せずに作られて設定された飛行機が鳥人間コンテストで琵琶湖に落ちるのを見て悲しくなったからというのもある。何ワットで素晴らしい設計です!と言いながらまっすぐ飛べずに落ちる飛行機は果たしていい飛行機だろうか。
御託を並べると単なる老害になってしまうので、最近読んでいる本に書いてあった練習問題のパラメタを人力飛行機用にややアレンジして練習問題をこの日記にひとつずつ載せていきたいと思う。そうすることで池ポチャする飛行機がひとつでももし減ったらそれほどうれしいことはない。
練習問題1 縦トリム
次の諸元の人力飛行機について、速度を6m/sから12m/sまで変化させたときに飛行機をトリムさせるために必要な水平尾翼の舵角および機体の迎角を求めよ。諸元はWindnautsのWebsiteから2011年の機体から引用させて頂きました。
- 主翼の面積 \(S_w\)=311 ft2
- 翼幅\(b_w\)=110 ft
- 主翼の揚力係数傾斜\(C_{LW_{\alpha}}\)=5.79
- 主翼のゼロ揚力角\(\alpha_{L0W}\)=-6.5 deg
- 主翼の取り付け角\(i_W\)=4.2deg
- 主翼の空力中心周りのピッチングモーメント係数\(C_{mW}\)=-0.14
- 水平尾翼の面積\(S_h\)=22 ft2
- 水平尾翼の翼幅\(b_h\)=12 ft
- 水平尾翼の揚力係数傾斜\(C_{Lh_{\alpha}}\)=4.93
- 主翼空力中心から重心までの距離\(l_w\)=0.31 ft
- 主翼空力中心から水平尾翼空力中心までの距離\(l_h\)=17 ft
- 重量\(W\)=212 lbs
ただし、下記の仮定を用いてよい。
- 水平尾翼の翼型は対称である
- 水平尾翼全体が回転するフライングテールの機体である
- 機体重心は主翼の空力中心より後ろにある
- 主翼の空力中心および水平尾翼の空力中心は胴体の基準線上にある。
- 機体の迎角は胴体の基準線から測る。
- プロペラが起こす推力に起因するモーメントは無視できる
- 胴体が起こすピッチングモーメントは無視できる
- 尾翼効率\(\eta_h\)は1としてよい。ここで、尾翼効率は一様流の動圧と水平尾翼の動圧の比である。
- 水平尾翼に当たる吹きおろしは、下記の通り与えられる
$$\epsilon_{d}=0.6\frac{C_{L_{W}}}{R_{A_{W}}}$$
- 水平飛行時の揚力方向の力のつり合いおよびピッチングモーメントのつり合いは下記の式で与えられる。画面が小さくて式が後ろまで表示されない場合は、携帯の場合は横にすれば見える。パソコンで見れば問題なく表示されるので試してみてほしい。
$$C_{LW_{\alpha}}(\alpha + i_{W} – \alpha_{L0W}) + \frac{S_h}{S_W}\eta_{h} C_{Lh_{\alpha}}[(1-\epsilon_{d_{\alpha}}) \alpha + i_{h} – \epsilon_{d0}]=\frac{W}{\frac{1}{2} \rho V^2_{\infty} S_{W}}$$
$$C_{mW}-\frac{l_W}{\overline{c}_W} C_{LW_{\alpha}}(\alpha + i_{W} – \alpha_{L0W}) -\frac{S_h l_h}{S_W \overline{c}_W} \eta_h C_{Lh_{\alpha}}[(1-\epsilon_{d_{\alpha}}) \alpha + i_{h} – \epsilon_{d0}]=0$$
ここで、
- \(i_{h}\): 水平尾翼取り付け角
- \(\overline{c}_W\): 主翼平均翼弦
解答は下記より見られるけれど、自分でちょっと解いてみてください。
解答
上記の揚力方向のつり合いの式およびピッチングモーメントのつり合いの式を整理すると、
$$
\left[
\begin{array}{ccc}
C_{L_{\alpha}}& C_{L_{i_{h}}}\\
C_{m_{\alpha}}& C_{m_{i_{h}}}
\end{array}
\right]
\left[
\begin{array}{ccc}
\alpha \\
i_h
\end{array}
\right]
=
\left[
\begin{array}{ccc}
C_W – C_{L0}\\
-C_{m0}
\end{array}
\right]
$$
ここで、
$$C_{L_{\alpha}}=C_{LW_{\alpha}}+\frac{S_h}{S_W}\eta_{h} C_{Lh_{\alpha}}(1-\epsilon_{d_{\alpha}})$$
$$C_{L_{i_{h}}}=\frac{S_h}{S_W}\eta_{h} C_{Lh_{\alpha}}$$
$$C_{m_{\alpha}}=\frac{l_W}{\overline{c}_W} C_{LW_{\alpha}} +\frac{S_h l_h}{S_W \overline{c}_W} \eta_h C_{Lh_{\alpha}}(1-\epsilon_{d_{\alpha}})$$
$$ C_{m_{i_{h}}}=\frac{S_h l_h}{S_W \overline{c}_W} \eta_h C_{Lh_{\alpha}}$$
$$C_W=\frac{W}{\frac{1}{2} \rho V^2_{\infty} S_{W}}$$
$$C_{L0}=C_{LW_{\alpha}}(i_W-\alpha_{L0W})-\frac{S_h}{S_W}\eta_{h} C_{Lh_{\alpha}} \epsilon_{d0}$$
$$C_{m0}=C_{mW} – \frac{l_W}{\overline{c}_W} C_{LW_{\alpha}}(i_W-\alpha_{L0W})-\frac{S_h l_h}{S_W \overline{c}_W}\epsilon_{d0}$$
吹きおろし傾斜\(\epsilon_{d_{\alpha}}\)を求めるため、与えられた吹きおろしの式を偏微分すると、
$$\epsilon_{d_{\alpha}}=\frac{\partial \epsilon_d}{\partial \alpha}=0.6\frac{1}{R_{A_{W}}} \frac{\partial C_{LW}}{\partial \alpha}=0.6\frac{C_{LW_{\alpha}}}{R_{A_{W}}}$$
また、\(\alpha=0\)での吹きおろし\(\epsilon_{d0}\)は、次の式により求まる。
$$\epsilon_{d0}=0.6\frac{C_{LW_{\alpha}} (i_W-\alpha_{L0W})}{R_{A_{W}}}$$
上記より、数値を代入して次式を得る。
$$
\left[
\begin{array}{ccc}
6.11& 0.349\\
1.27& 2.10
\end{array}
\right]
\left[
\begin{array}{ccc}
\alpha \\
i_h
\end{array}
\right]
=
\left[
\begin{array}{ccc}
C_W-1.08\\
-0.0143
\end{array}
\right]
$$
これを解いて、
$$
\left[
\begin{array}{ccc}
\alpha\\
i_h
\end{array}
\right]
=
\left[
\begin{array}{ccc}
0.170C_W-0.182\\
-0.103C_W+0.104
\end{array}
\right]
$$
問題で与えられた速度範囲での\(C_W\)を計算して上記の式に入れ、\(\alpha\)および\(i_h\)を求めると、次のプロットを得る。
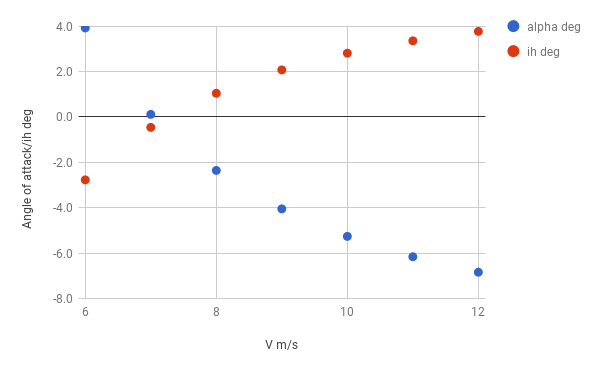
上記の数値、たとえば揚力傾斜とか吹きおろしは適当だが、そこそこそれっぽい値に一見見える。8m/sでトリムしていて、そこから6m/sまで減速したいときは水平尾翼を4degくらい水平尾翼後縁下げしないといけないということがわかる。計算間違ってるかもしれないので、もしそうなら教えてください。
元の問題はもっと示唆に富んだ面白い問題だったのだが、エレベータがないこと、および重心がすでに決まっている実機を参考にしたため、単に解くだけの問題となってしまった。それでもこのトリムの感覚を身につけるとだいぶ変わるのではないかと思う。
第2回はこちら。
参考図書は下記。アメリカ版を買うと高いが、インド版を買うと安い。



コメント
[…] 前回は人力飛行機が速度を変えるためにどの程度の水平尾翼の舵角が必要であるかということを計算した。今回は前回のおまけとして、前回の問題にかぶせて簡単な追加問題を書いてみ […]